|
When verifying the scalability of computer programs, it is always helpful to have large data sets available as input. Imagine for instance that you've been given the task of testing a new word processing program with thousand page documents. The first thing to try would be copying a one page document and pasting it a thousand times into a new empty document. This would certainly qualify as a thousand page document, but might not represent the variety and complexity of a real world test case. Now consider the problem of stress testing parsers in general, and compilers in particular. It's not hard to write simple test cases of one or a few lines for individual requirements. But how to simulate submitting large user programs without actually having access to real source code? What's needed is a technique that can randomly populate a source file of arbitrary size with nonsense statements that meet all the syntactical, grammatical, lexical, and semantic constraints of the software under test.
On this page I explain just such a technique using a composite tree model for source code generation, with working examples posted for free download in a variety of computer languages. In some cases I've used a given language to generate code for the language itself, although in fact one can use almost any language to generate code for any other language. The work presented here is derived from a more complex project I was involved in some years back, in which we developed a cross-compiler to build a processor memory image for an embedded target that included data files, hardware configuration files, and executable code files. The source code was a binary representation of a visual programming language called "ladder logic", which is used in industrial control systems.
When generating test cases it is important to keep in mind what sorts of defects one expects to find. The obvious ones are missing implementation, wrong implementation, and extra implementation, when compared to documented requirements. That's right, features which are not required are defects, when testing software that's meant to be very robust like compilers. But then there are always implied requirements. One is that a compiler should always accept and generate code for any input that is valid according to the compiler's rules, no matter how nonsensical the logic may be. Another is that a compiler should never accept or generate code for any input that is not valid according to the compiler's rules, no matter how plausible the logic may be. And one would hope that a compiler never crashes no matter what sort of input you feed in, but rather exits gracefully in all cases and reports faithfully what happened.
Before digging into the code, let's review the details of composite tree structures. Part of the more general category of structures known as acyclic directed graphs (ADGs), the composite tree is simply a list of lists. That is, the root node is an object which may contain a list of zero or more objects, each of which may also contain a list of zero or more objects, and so on. Nodes may be either composite if they do contain a list of subordinate objects, or terminal if they have no subordinates. These are often called "branch nodes" and "leaf nodes", respectively. In object-oriented terms, the nodes on a composite tree are "polymorphic", because while they can be of many different types, they must all adhere to a common interface.
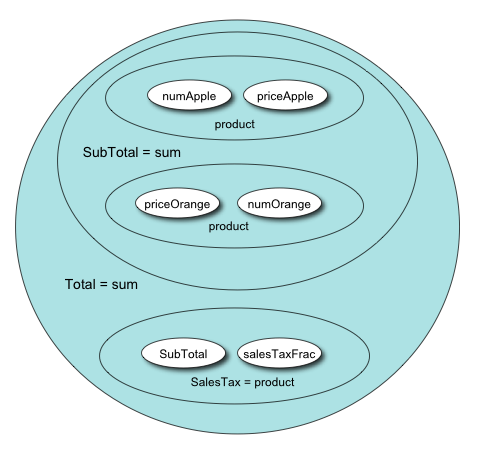
Consider a simple example that represents a math expression used to total up the selling price of some goods at a fruit stand. In words, we would say that one multiplies the number of apples times the price/each for apples, multiplies the number of oranges times the price/each for oranges, sums the two products to form a subtotal, and then adds in the sales tax which is the product of the subtotal times a constant factor. In outline form the steps might look like this:
The outline form then maps directly to a math expression which captures the structure of the outline by wrapping operations in parentheses. Symbolic names are used here to represent the actual values.
Total = (Subtotal = (numApple * priceEachApple) + (numOrange * priceEachOrange))
+ (Subtotal * SalesTaxFactor)
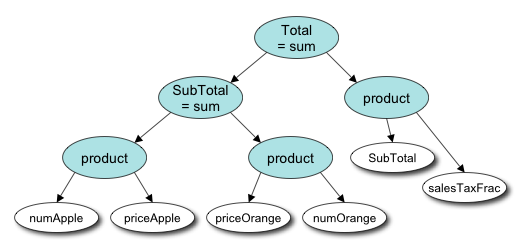
The mapping works in either direction since both representations contain the same information. Note that even though this expression contains only addition and multiplication, the order of execution matters due to the assignment operator on the right-hand side. An important attribute of composite trees is that the order in which subordinate nodes are scanned is preserved. Now we look in Fig. 2 at a visual representation of the same expression which encodes the idea of operators owning their operands by enclosing them within a boundary, as so-called nested sets. (Graphics in Fig. 2 and Fig. 3 are adapted from Wirth[1986], and Knuth[1973])
|
Unfortunately, enclosing nodes within a containing object doesn't immediately define a path or order in which the nodes are visited. So now we look in Fig. 3 at a different visual representation which suggests the use of pointers or references, drawn as arrows, to maintain the tree structure. In this view we can follow the path of execution by following the arrows to visit each node in turn, scanning from left to right. We start by asking the top node (the "root" node) for its value. The "Total" node obtains its sum by asking for the value of each of its subordinates, each of which then asks for the value of each of their subordinates, and so on. After every node has been visited, the total sum can be obtained. Following this path is commonly called "recursive descent".
|
The reference model in fact maps directly to the outline and math expression forms shown above, and to the object-oriented representations expressed in the code examples given below. Any of these models can be converted into any other, without ambiguity or loss of information. Conversion to a one-dimensional form, required for persistent storage, is called "serialization", while recovering the tree structure from a one-dimensional representation is called "deserialization". In many cases, this is the job of the parser being tested.
In my first example, I use Visual Basic for Applications (VBA) running inside an Excel macro to generate valid Excel math statements which are used to populate an Excel worksheet. This may seem trivial, since Excel statements are interpreted, not compiled, but it actually demonstrates all the features of using a composite tree model to generate statements that conform to rules of grammar and syntax. As you'll see, Excel is well suited for use as a table-driven code generator.
Excel/VBA Test Case Generator (78kB Excel Worksheet File)
Table 1. Excel/VBA Module Interface
Notice that the Populate method has the same interface in both class modules, as does the Express method. So these methods can be called against any class object that happens to be part of the Collection data member in the Branch class module. VBA doesn't check until run time if these methods actually exist for every object in the composite tree. Method arguments are shown in parentheses here in the module definition, but must be given without parentheses when they appear elsewhere in the code to allow VBA to pass them by reference, as required in my implementation.
In my second example, I use a C language command line utility to spit out valid C language math expressions, drawing operands and operators from two text files which are named on the command line. The output can be compiled without error, as you'll see in the source files download package.
C Language Test Case Generator (5kB Zip File)
Table 2. C Language Struct Interface /* CompTree.h is the header for a command line utility which */ /* demonstrates use of a C program as a code generator. */ enum nodeType { branch, leaf }; typedef struct node nodeStruct; /* composite tree is made up of node structs, arranged in linked lists */ struct node { /* data members common to all nodes */ enum nodeType theType; nodeStruct *next; /* list at my level */ /* data members for branch node */ nodeStruct *list; /* list beneath my level */ char pre[32]; char inter[32]; char post[32]; /* data members for leaf node */ char name[32]; int myDepth; }; /* method members which operate on node structs */ void populate(nodeStruct *theNodePtr, int *theDepthPtr, int *nodeCountPtr); void express (nodeStruct *theNodePtr, int *maxDepthPtr); void release (nodeStruct *theNodePtr, int *nodeCountPtr);
In the C language, one self-referencing typedef does it all. Different behaviors are controlled by an enum, which results in long switch statements in each of the method members. A new method member is added here to free memory allocated for the nodes, which wasn't necessary in the VBA code.
In this example, I use a C++ command line utility to create valid XML statements, drawing tags and data from two text files named on the command line. Most modern web browsers have built-in XML viewers which you can use to study the output.
C++ Language Test Case Generator (4kB Zip File)
Table 3. C++ Language Class Interface // File named 'XompTree.h' is the header file for demo // of binary tree graph, used to simulate user inputs. // abstract base class to compose objects into a tree structure class node { public: static int theDepth; static int nodeCount; static int maxDepth; virtual ~node(); // pure virtual functions virtual void populate() = 0; virtual void express(ostream &) = 0; };// composite class, may have child nodes class brnch: public node { private: char pre[32]; char inter[32]; char post[32]; list<node *> the_list; public: static fileStream brnchFile; ~brnch(); void populate(); void express(ostream &); };// component class, no child nodes class leaf: public node { private: char the_str[32]; int myDepth; public: static fileStream leafFile; leaf(); ~leaf(); void populate(); void express(ostream &); };
Here a list template is used to maintain the list within a list. While I've tried to follow the idioms of each language, C++ is clearly the most expressive when defining the composite tree structure.
In my final example, I use a Python script to generate valid JSON text, drawing key names and values from a text file named on the command line. Some web browsers have JSON viewers which you can use to study the output. This capability is also available in many IDEs and editors. Notepad++, for instance, has an optional JSON Viewer plugin.
Python Test Case Generator (6kB Zip File)
Table 4. Python Class Interface # base class for tree nodes # implementation details not shown here... class node: # class variables theDepth = 0 nodeCount = 0 maxDepth = 0 # instance methods def Populate(self):# subclass for dictionary branch nodes # implementation details not shown here... class dBranch(node): def __init__(self): # add key-value pair to dictionary def AddToList(self, newItem): # serialize as Json text on console def Express(self):# subclass for array branch nodes # implementation details not shown here... class aBranch(node): def __init__(self): # add value to array def AddToList(self, newItem): # serialize as Json text on console def Express(self):# subclass for tree leaf nodes # implementation details not shown here... class leaf(node): def __init__(self): # obtain content from input file def Populate(self): # serialize as Json text on console def Express(self):
Python, as a scripting language, is ideal for trying out ideas and prototyping a proof-of-concept for your next compiler test case generator. Now we've seen example programs written in a variety of languages, both compiled and interpreted, which produce bulk random test cases according to a composite tree model. These can be used to validate the performance and scalability of parsers and compilers. In addition, these test cases can also be designed to validate the serialization, transmission, and deserialization of structured text including JSON and XML. I feel better already, how about you?
I am placing the ideas presented on this page in the public domain, for the benefit of software developers and engineers. Please remember that only you can determine if these ideas are suitable for your application. The burden is on you to verify, through functional test, code inspection, and any other means you determine is appropriate, whether the code presented here actually works or not. And only you know if you are qualified to make modifications to the source code presented here. Feel free to post a link to this page on your site, but please don't copy my content. This page should be available at this URL for the foreseeable future. I claim a trademark interest in the names "Williamsonic" and "www.williamsonic.com".