| BPF | R1 | R2 | C1 | C2 |
|---|---|---|---|---|
| First Section |
4.4 kOhms | 44 kOhms | .056 uF | .056 uF |
| Second Section |
2.4 kOhms | 24 kOhms | .056 uF | .056 uF |
This applet accepts transfer function coefficients as input, and calculates magnitude and phase response over a range of frequencies. A new version is now available which lets you set the start frequency and choose units for the horizontal axis.
The Bode Plot or Bode Diagram 1 is a convenient way to represent the steady state frequency response of an electronic filter. Here, amplitude response is plotted in blue with logarithmic frequency in the horizontal axis over a 2 decade range, against a logarithmic scale of 5 dB per division in the vertical axis. Phase response is plotted in magenta against a linear scale of π/4 radians, or 45° per division in the vertical axis. Follow these steps to use the applet:
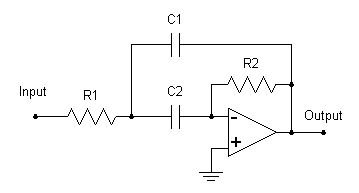
To illustrate how to use the Bode Plot Applet, I've taken an example from Don Lancaster2. The design is an octave-wide fourth order bandpass filter covering the range from 200 Hz to 400 Hz. The filter is implemented as two cascaded second order bandpass filter sections with their center frequencies shifted up and down from the nominal center frequency of 277 Hz by a ratio of 1.35:1. Each of the two sections is a multiple feedback filter built around an opamp as shown in the schematic diagram. Resistor and capacitor values for each section are shown in the table.
 |
|
Mr. Lancaster gives the transfer function for each section as:
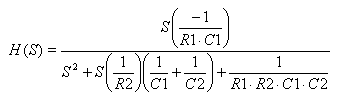
Plug in the actual values to obtain the transfer function coefficients for each filter section.
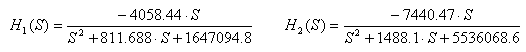
Before plotting the frequency response however, we need to normalize the coefficients to a center frequency of 1 radian/second. This is done by multiplying S by (2π fc) wherever it appears3. The nominal center frequency of the finished filter is 277 Hz, so we multiply S by 1740.44.
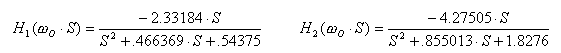
This finally gives us the coefficients we need to plot the normalized frequency response of the complete filter. Copy these numbers into the applet's Numerator and Denominator fields and click the [Calculate Plot] button to see the result.
| First Section | Second Section | Both Sections | |
|---|---|---|---|
| Numerator | -2.33184, 0 | -4.27505, 0 | (-2.33184, 0)(-4.27505, 0) |
| Denominator | 1, .466369, .54375 | 1, .855013, 1.8276 | (1, .466369, .54375)(1, .855013, 1.8276) |
To verify the accuracy of the Bode Plot Applet, I gathered a bunch of components and plugged them into my breadboard with a pair of TL082 dual opamps. I used parallel and series combinations to get close to the specified resistance and capacitance values, but was still 5% to 10% off on center frequency for each second order section. I then reduced the values of R1 and put trimmer potentiometers in series. Since the characteristics of each filter section rely in part on the source impedance seen by the section, I made sure to drive each filter section from another TL082 output. To accomplish this, I connected one opamp as a unity gain follower to serve as an input buffer.

Using the trimmers, I set the center frequency of each filter section to its nominal value, 205 Hz in the first section and 375 Hz in the second. You could do this by peaking the amplitude response at the center frequency, but it is much easier to connect the input and output of the filter section you are trimming to the X and Y inputs of an oscilloscope to obtain a Lissajous pattern. Then just trim the filter for exactly 180° phase shift (ellipse closes to a single diagonal line) when driven at the desired center frequency.
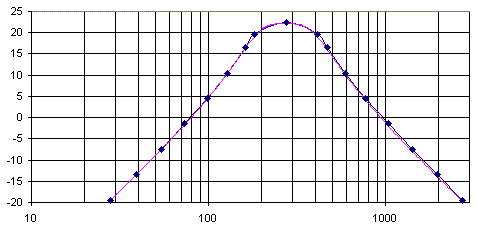
After this simple tuneup, I measured the overall amplitude response of the completed filter and plotted the results in MS Excel. The following screen shot from Excel shows the measured points as blue diamonds. For comparison, I pasted the predicted values from the Bode Plot Applet into Excel, shown below in magenta. As you can see, the agreement between predicted gain and actual measured results is almost perfect.